Hugging Face is the GitHub of AI models. It uses git with LFS (and xet) to serve large model weights, but at the end of the day, you can’t use those weights directly. The code required to run them is typically implemented in popular Python packages like transformers (for LLMs) or diffusers (for diffusion models).
In this blog post, I will explain how to take a model weights file and use it to generate your very first token using your own custom inference implementation. Let’s get started—this will be quite technical and will likely involve some math! While it is always helpful to have a background in AI and ML, you can still follow along without it.
For simplicity, I will implement the smallest model in the Qwen3 family: Qwen3-0.6B. My implementation will not include any optimizations, as our aim is not to replace existing libraries but simply to learn.
An ML Framework
We will need an ML framework because we have to perform numerous tensor operations; unless you are feeling lucky, you likely won’t want to implement those by hand. Another benefit of using a framework is that common operations such as Linear layers, Embedding layers, and activation functions are already implemented and optimized for various hardware, including CUDA, Metal, and CPUs.
For this blog, I will stick with Candle - A minimalist ML framework in Rust.
Architecture
Finding the architecture is the first step in implementing a model. Unless you want to read the research paper released alongside the model, I believe the best way to find the architecture for any model is to look at the implementation code in transformers. Here, you can find all the models and their respective implementations.
However, another convenient way to find a model’s components is to simply print the model object itself.
from transformers import AutoModel
model_name = "Qwen/Qwen3-0.6B"
model = AutoModel.from_pretrained(model_name)
print(model)
Qwen3Model(
(embed_tokens): Embedding(151936, 1024)
(layers): ModuleList(
(0-27): 28 x Qwen3DecoderLayer(
(self_attn): Qwen3Attention(
(q_proj): Linear(in_features=1024, out_features=2048, bias=False)
(k_proj): Linear(in_features=1024, out_features=1024, bias=False)
(v_proj): Linear(in_features=1024, out_features=1024, bias=False)
(o_proj): Linear(in_features=2048, out_features=1024, bias=False)
(q_norm): Qwen3RMSNorm((128,), eps=1e-06)
(k_norm): Qwen3RMSNorm((128,), eps=1e-06)
)
(mlp): Qwen3MLP(
(gate_proj): Linear(in_features=1024, out_features=3072, bias=False)
(up_proj): Linear(in_features=1024, out_features=3072, bias=False)
(down_proj): Linear(in_features=3072, out_features=1024, bias=False)
(act_fn): SiLUActivation()
)
(input_layernorm): Qwen3RMSNorm((1024,), eps=1e-06)
(post_attention_layernorm): Qwen3RMSNorm((1024,), eps=1e-06)
)
)
(norm): Qwen3RMSNorm((1024,), eps=1e-06)
(rotary_emb): Qwen3RotaryEmbedding()
)
It can be overwhelming at first, but here is a simple breakdown of the architecture:
The model consists of:
- Token Embedding: Features a vocabulary size of 151,936 with 1,024 hidden dimensions.
- Layers: This section contains the core transformer blocks.
- 28 Transformer Decoder Layers, each consisting of:
- An Attention Layer
- An MLP (Multi-Layer Perceptron) Layer
- A Normalization Layer (RMSNorm)
- 28 Transformer Decoder Layers, each consisting of:
- Final Normalization Layer
- Rotary Positional Embeddings (RoPE)
This gives you a rough idea of the tensor sizes and their relationships. Here is a very high-level overview of each component:
Embedding
Each token needs to be converted into a feature vector. An embedding table is used to map a token ID to its corresponding vector. Typically, a tokenizer processes the text and provides IDs for each token; in the case of Qwen3, these IDs range from 0 to 151936. The embedding matrix then maps each of these token IDs into a 1024-dimensional vector space.
We can also use the transpose of this embedding matrix to map a feature vector back into its token ID at the end of the model’s processing. This technique is known as
tied_word_embeddings.
Linear
A Linear layer is essentially a simple matrix multiplication. For example, a q_proj with a shape of (1024, 2048) represents the weight matrix in our operation.
This operation is usually already implemented in most ML frameworks.
RMSNorm
Root Mean Square Normalization (RMSNorm), as the name implies, is a normalization step where we first calculate the square of all elements in the vector, find the mean of those squares, and then take the square root of that mean. We then divide all the elements of the original vector by this value.
Mathematically,
$$ y_i = \frac{x_i}{RMS(x)} $$where
$$ RMS(x) = \sqrt{\frac{1}{d} \sum_{i = 1}^{d}{x_i}^2} $$This operation is usually already implemented in most ML frameworks.
SiLU - Sigmoid Linear Unit
It’s an activation function and mathematically defined as
$$ SiLU(x) = \frac{x}{1 + e^{-x}} $$Self Attention
Scaled dot product attention, mathematically defined as
$$ Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}}) V $$For more information on this read this awesome blog
This operation is usually already implemented in most ML frameworks.
Rotary Position Embedding
Since embedding and attention mechanisms only map tokens to vectors, they do not inherently capture positional information. For instance:
“I bound an Apple Watch”
“Watch I bought an Apple”
They can use exactly the same words but have a completely different meaning based on the position of those words. In order to capture this, we need to encode the position of words in a sentence. Qwen3 uses Rotary Positional Encoding (RoPE); for each pair of dimensions in an embedding, RoPE treats them as coordinates in 2D space and rotates them by an angle θ proportional to the token’s position.
Read more about it here (it’s a lot of maths!!)
This is not implemented in the Candle framework, and since it involves complex mathematics, I will skip the specific implementation details for now
Exploring the Weights
Now that we have a basic understanding of the model, let’s examine the weights themselves. Weights are typically provided in the safetensors format on Hugging Face. When you select a weights file, you can usually view the tensor metadata, including the name, size, and precision of each parameter.
You can check it yourself here. Since this is a small model, all of its weights are stored in a single file; for larger models, the weights are typically sharded across multiple files.

The weights are arranged in a tree-like format for each layer. The top-level model object stores all the model’s weights, following the same naming conventions and tensor shapes as the model architecture we previously discussed.
To bring the model to life, we need to define the implementation structure in our code and “mount” the loaded tensor weights onto the corresponding layers. In frameworks like Candle, this is typically handled by a VarBuilder, which acts as a bridge between the safetensors file and your model’s variables.
Implementation
To build the model correctly, we must construct it from the ground up—working from the “leaf” components to the “root” structure. For instance, to implement the Qwen3MLP, we first need the Linear and SiLUActivation components. Fortunately, both are standard building blocks already available in our ML framework.
Let’s get into implementation!
Qwen3MLP
Qwen3 utilizes a Gated Linear Unit (GLU), which, when combined with the SiLU activation function, is known as SwiGLU. This architecture differs from a standard MLP because it incorporates a “gate” to filter information, effectively suppressing unwanted activations and allowing only the most relevant features to pass through.
In SwiGLU, the process involves two parallel linear transformations:
- One path applies the SiLU activation (the “gate”).
- The other path remains linear.
- The two paths are multiplied element-wise before the final projection.
Fortunately, its implementation is much simpler
pub struct Qwen3MLP {
gate: Linear,
down: Linear,
up: Linear,
}
impl Qwen3MLP {
pub fn new(vb: VarBuilder) -> Result<Self> {
let gate = linear_no_bias(1024, 3072, vb.pp("gate_proj"))?;
let down = linear_no_bias(3072, 1024, vb.pp("down_proj"))?;
let up = linear_no_bias(1024, 3072, vb.pp("up_proj"))?;
Ok(Self { gate, down, up })
}
pub fn forward(&self, xs: &Tensor) -> Result<Tensor> {
let gate = self.gate.forward(&xs)?;
let gate_silu = silu(&gate)?;
let up = self.up.forward(&xs)?;
let intermediate = (gate_silu * up)?;
self.down.forward(&intermediate)
}
}
In this case, linear_no_bias and silu are functions from our ML framework. They automatically read the required tensors from the VarBuilder based on the specified shapes and names, then construct the functional layers for us.
The expression vb.pp("context") creates a nested VarBuilder within that specific namespace. To retrieve a weight, you call vb.get((shape), "name"), which looks for the tensor named "name" within the current context—essentially matching the "context.name" path seen in the Hugging Face safetensors explorer.
Qwen3Attention and Qwen3RotaryEmbedding
Qwen3 utilizes Grouped Query Attention (GQA), which implies that our framework’s attention mechanism must explicitly support this configuration. We will be using our framework’s built-in implementation of attention to handle this efficiently.
The input tensor to this block always has the shape [BatchSize, Sequence, HiddenSize], where HiddenSize represents the embedding feature dimension in this case, 1024. To apply Self-Attention and RoPE, we must reshaped the tensor to expose its individual attention heads. According to the Qwen3-0.6B config.json, the model uses 16 query heads and 8 key-value heads, with each head having a dimension of 128.
During the attention calculation, the HiddenSize (1024) is split:
- Query (Q): 16 heads × 128 dim = 2048 (total projection size)
- Key/Value (KV): 8 heads × 128 dim = 1024 (total projection size)
pub struct Qwen3Attention {
k_proj: Linear,
q_proj: Linear,
v_proj: Linear,
o_proj: Linear,
q_norm: RmsNorm,
k_norm: RmsNorm,
rope: Qwen3RotaryEmbedding,
head_dim: usize, // Dimention of attention head. Fixed to 128
}
We then initialize the weights of each component.
impl Qwen3Attention {
pub fn new(vb: VarBuilder) -> Result<Self> {
let k_proj = linear_no_bias(1024, 1024, vb.pp("k_proj"))?;
let q_proj = linear_no_bias(1024, 2048, vb.pp("q_proj"))?;
let v_proj = linear_no_bias(1024, 1024, vb.pp("v_proj"))?;
let o_proj = linear_no_bias(2048, 1024, vb.pp("o_proj"))?;
let q_norm = rms_norm(128, 1e-06, vb.pp("q_norm"))?; // eps is 1e-06
let k_norm = rms_norm(128, 1e-06, vb.pp("k_norm"))?; // eps is 1e-06
let device = Device::Cpu; // Device::new_cuda(0)? for NVIDIA
Ok(Self {
k_proj,
q_proj,
v_proj,
o_proj,
q_norm,
k_norm,
rope: Qwen3RotaryEmbedding::new(128, 32000, 1_000_000.0, &device)?,
head_dim: 128,
})
}
}
Many of the specific constants required for these layers such as the RoPE theta base (θ), the RMSNorm epsilon (ϵ), and the number of layers are defined in the model’s config.json. While these are customizable parameters, I have kept them hard-coded in this implementation to keep the code focused and easy to follow.
In the forward(...) we define the forward pass of this layer.
impl Qwen3Attention {
pub fn forward(&mut self, xs: &Tensor, positions: &Tensor) -> Result<Tensor>{
// xs: [Batch, Seq, hidden_state]
let (batch, seq, hidden) = xs.shape().dims3()?;
// xs: [Batch, Seq, num_heads, head_dim] num_head is infered
let hidden_shape = (batch, seq, (), self.head_dim);
let query_layer = self.q_proj.forward(xs)?.reshape(hidden_shape)?;
let key_layer = self.k_proj.forward(xs)?.reshape(hidden_shape)?;
let val_states = self.v_proj.forward(xs)?.reshape(hidden_shape)?;
// [Batch, num_heads, Seq, head_dim]
let query_states = self.q_norm.forward(&query_layer)?.transpose(1, 2)?;
let key_states = self.k_norm.forward(&key_layer)?.transpose(1, 2)?;
let (query_states, key_states) =
self.rope.forward(&query_states, &key_states, positions)?;
let query_states = query_states.transpose(1, 2)?.contiguous()?;
let key_states = key_states.transpose(1, 2)?.contiguous()?;
// Attention Is All I need!
// This is Flash Attention 2 implementation from Candle ML Framework
// We use causal masking and softmax dot product scaling attention
let attn_out = flash_attn(
&query_states,
&key_states,
&val_states,
(self.head_dim as f32).powf(-0.5), // Softmax scaling
true, // Causal
)?
.reshape((batch, seq, ()))?;
self.o_proj.forward(&attn_out)
}
}
We call the forward of various building blocks in this self attention. The order of operation is derived by looking into the implementation of the transformers library.
RoPE needs shape in the format [BatchSize, NumHeads, Sequence, HeadDim] which is why we reshape the queries and keys and later reshape them to original shape.
Flash Attention 3 implementations often require specific tensor layouts for peak performance. In our case, we are utilizing Flash Attention 2, which expects the input tensor in the shape
[BatchSize, Sequence, NumHeads, HeadDim]. When building your own model, you should always consult your specific attention implementation to verify the exact input dimensions it requires.
Rotary Positional Encoding (RoPE) can be conceptually complex, so to keep this post concise, I have documented the full implementation in a GitHub Gist with detailed comments. The core idea is efficiency: to support the maximum context window without constant re-computation, we precompute a “lookup table” of sine and cosine rotary tensors. During inference, we simply apply these rotations to the Query and Key tensors based on the specific position of each token in the sequence.
Qwen3Decoder
Decoder combines attentions and MLP layers together with pre and post normalization. This layer is repeated for 27 times and called layers in the above components tree. Its implementation is very simple.
pub struct Qwen3Decoder {
mlp: Qwen3MLP,
attention: Qwen3Attention,
input_norm: RmsNorm,
post_attn_norm: RmsNorm,
}
impl Qwen3Decoder {
pub fn new(vb: VarBuilder) -> Result<Self> {
let input_norm = rms_norm(1024, 1e-06, vb.pp("input_layernorm"))?;
let post_attn_norm = rms_norm(1024, 1e-06, vb.pp("post_attention_layernorm"))?;
let mlp = Qwen3MLP::new(vb.pp("mlp"))?;
let attention = Qwen3Attention::new(vb.pp("self_attn"))?;
Ok(Self {
input_norm,
post_attn_norm,
mlp,
attention,
})
}
}
The forward(...) implementation of the decoder layer is particularly interesting because it utilizes a “dual residual” architecture. The first bypasses the Attention block, and the second bypasses the MLP block. This design, often referred to as a “Pre-Norm” transformer block, ensures that the original input signal can flow through the entire stack, which helps prevent the vanishing gradient problem and stabilizes the model’s internal activations.
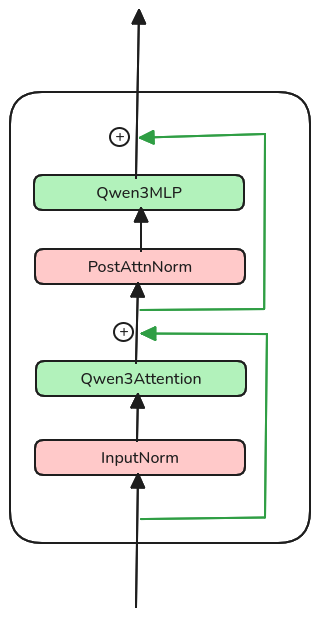
In code it translates to
impl Qwen3Decoder {
pub fn forward(&self, xs: &Tensor, positions: &Tensor) -> Result<Tensor>{
let residual = xs.clone();
let hidden_state = self.input_layernorm.forward(xs)?;
let hidden_state = self.attention.forward(&hidden_state, positions)?;
let hidden_state = (residual + hidden_state)?;
let residual = hidden_state.clone();
let hidden_state = self.post_attention_layernorm.forward(&hidden_state)?;
let hidden_state = self.mlp.forward(&hidden_state)?;
residual + hidden_state
}
}
Finally - Qwen3 Model Implementation
Now we have all the building blocks for implementing the Qwen3 model we just need to piece them together let’s see how that is done.
pub struct Qwen3Model {
embedding: Embedding,
layers: Vec<Qwen3Decoder>,
norm: RmsNorm,
lm_head: Linear,
}
impl Qwen3Model {
pub fn new(vb: VarBuilder) -> Result<Self> {
let embedding = embedding(151936, 1024, vb.pp("embed_tokens"))?;
let layers = (0..28usize)
.map(|i| Qwen3Decoder::new(vb.pp("layers").pp(i)).unwrap())
.collect();
let norm = rms_norm(1024, 1e-06, vb.pp("norm"))?;
let lm_head = linear_no_bias(1024, 151936, vb.root().pp("lm_head"))?;
Ok(Self {
norm,
layers,
embedding,
lm_head,
})
}
pub fn forward(&self, input_ids: Tensor, pos: Tensor) -> Result<Tensor> {
let mut hidden_state = self.embedding.forward(&input_ids)?;
for l in self.layers.iter_mut() {
hidden_state = l.forward(&hidden_state, &pos)?;
}
let hidden_state = self.norm.forward(&hidden_state)?;
self.lm_head.forward(&hidden_state)
}
}
input_ids is the tensor containing the input token IDs and position contains the position of the tokens in the sequence. Result of this model’s forward pass is [BatchSize, Sequence, HiddenState] and the next token is in the last sequence of each batch.
Running our Model
Tokenising the prompt
In order to produce some output, we need to first tokenise the input text, for this we will use tokenizers crate from hugging face and to download weights from hugging face we will use the hf_hub crate, we need to encode the tokens into a vector of token ids.
let api = Api::new()?;
let model = api.model(String::from("Qwen/Qwen3-0.6B"));
let tokenizer = Tokenizer::from_file(model.get("tokenizer.json")?)?;
let encoding = tokenizer.encode("The capital of France is", false)?;
let encoding_tensor = Tensor::from_slice(encoding.get_ids(), (1, ()), &device)?;
The resulting encoding_tensor contains of shape (1, len(encoding)) contains all the indices of the tokens for the provided prompt.
Loading model weights and running
Now we need to load the weights into our model or essentially we need to build the VarBuilder, this uses mmap and hence inherts unsafe from there. We need to also create the position tensor which is a tensor in the shape filled with iota like sequenece.
let weights = model.get("model.safetensors")?;
let vb = unsafe {
VarBuilder::from_mmaped_safetensors(&[weights], DType::BF16, &device)
};
let (batch, seq_len) = encoding_tensor.dims2()?;
let positions = Tensor::arange(0u32, seq_len, &device)?.unsequeeze(0)?;
let model = Qwen3Model::new(vb.pp("model"))?;
let logits = model.forward(encoding_tensor, positions)?;
let last_logits = logits // [1, seq_len, vocab]
.narrow(1, seq - 1, 1)? // [1, 1, vocab]
.squeeze(0)? // [1, vocab]
.squeeze(0)? // [vocab]
.to_device(&Device::Cpu)? // Move to CPU for decoding
.to_dtype(DType::F32)?;
let next_id = sample_top_k(&last_logits, 50, 0.8, &mut rng)?;
let decoded = tokenizer.decode(&[next_id], true)?;
println!({decoded}); // Print Paris
We used proper sampling but you can even use greedy top sampler to get the same results, scope of sampling is outside this blog and shapes are documented in the code.
What’s next?
In the next blog, I will talk about how I used this implementation of Qwen3 along with Paged Attention to build a tiny vLLM implementation. This implementation is part of that project so I am not open sourcing the code, I will open source the code when the whole project is complete.